You are here: Foswiki>FEM Web>WindTurbine>BladeElementMomentum (01 Dec 2017, RobertoBernetti)Edit Attach
Froude’s momentum theory of propulsion
- inviscid,
- incompressible, and
- irrotational;and both
- the velocity and
- the static pressure are uniform over each cross section of the disk and stream-tube.
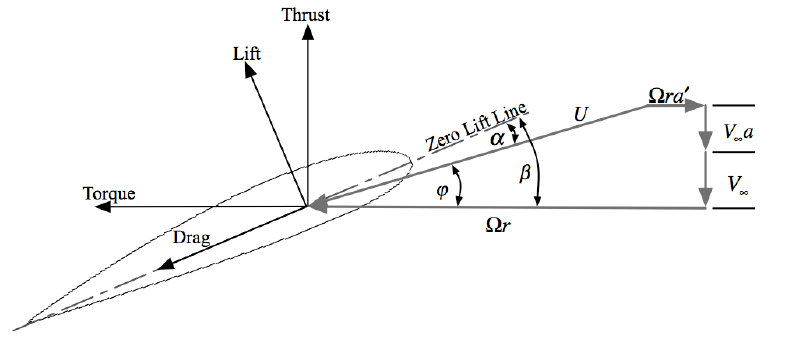
The contribution of each annulus to the total force and tordque is $$ \mathrm{d} T = \frac{1}{2} B \rho U^2 (C_L \cos \phi -C_D \sin \phi ) c \cdot \mathrm{d} r $$ $$ \mathrm{d} Q = \frac{1}{2} B \rho U^2 (C_L \sin \phi + C_D \cos \phi ) c \cdot r \cdot \mathrm{d} r $$
- Just as the annular stream-tube control volumes used in the slip-stream rotation analysis were assumed to be noninteracting [assumption (1)], it is assumed that there is no interaction between the analyses of each blade element
- The forces exerted on the blade elements by the flow stream are determined solely by the two-dimensional lift and drag characteristics of the blade element airfoil shape and orientation relative to the incoming flow.
 [1] Anders Ahlstrom, "Aeroelastic Simulation of Wind Turbine Dynamics", Doctoral Thesis, Royal Institute of Technology Sweden
[2] Lin Wanga,*, Xiongwei Liu b, Athanasios Koliosa, "State of the Art in the Aeroelasticity of Wind Turbine Blades: Aeroelastic Modelling", Renewable and Sustainable Energy Reviews, Volume 64, October 2016, pp 195-210 DOI:10.1016/j.rser.2016.06.007
[3] M. K. Rwigema "PROPELLER BLADE ELEMENT MOMENTUM THEORY WITH VORTEX WAKE DEFLECTION", 27TH INTERNATIONAL CONGRESS OF THE AERONAUTICAL SCIENCES
-- RobertoBernetti - 29 Nov 2017
[1] Anders Ahlstrom, "Aeroelastic Simulation of Wind Turbine Dynamics", Doctoral Thesis, Royal Institute of Technology Sweden
[2] Lin Wanga,*, Xiongwei Liu b, Athanasios Koliosa, "State of the Art in the Aeroelasticity of Wind Turbine Blades: Aeroelastic Modelling", Renewable and Sustainable Energy Reviews, Volume 64, October 2016, pp 195-210 DOI:10.1016/j.rser.2016.06.007
[3] M. K. Rwigema "PROPELLER BLADE ELEMENT MOMENTUM THEORY WITH VORTEX WAKE DEFLECTION", 27TH INTERNATIONAL CONGRESS OF THE AERONAUTICAL SCIENCES
-- RobertoBernetti - 29 Nov 2017
| I | Attachment | Action | Size | Date | Who | Comment |
|---|---|---|---|---|---|---|
| |
BladeForceVelocity.png | manage | 36 K | 01 Dec 2017 - 13:43 | RobertoBernetti |
Edit | Attach | Print version | History: r5 < r4 < r3 < r2 | Backlinks | View wiki text | Edit wiki text | More topic actions
Topic revision: r5 - 01 Dec 2017, RobertoBernetti
- Toolbox
-
 Create New Topic
Create New Topic
-
 Index
Index
-
 Search
Search
-
 Changes
Changes
-
 Notifications
Notifications
-
 RSS Feed
RSS Feed
-
 Statistics
Statistics
-
 Preferences
Preferences

This work is licensed under a Creative Commons Attribution-ShareAlike 3.0 Unported License1999-2025
Ideas, requests, problems regarding this site? Send feedback


