RenewalTheory

Poisson Process

From Wikipedia

The Poisson process is a collection

{K(t) : t \ge 0}

of random variables, where K(t) is the number of events that have occurred up to time t (starting from time 0). The number of events between time a and time b is given as

K(b)-K(a)

and has a Poisson distribution. Each realization of the process {N(t)} is a non-negative integer-valued step function that is non-decreasing, but for intuitive purposes it is usually easier to think of it as a point pattern on %$[0,\infty)$% (the points in time where the step function jumps, i.e. the points in time where an event occurs).

It can be derived by a limiting process from a Bernoulli sequence, considering the k-th occurence of the event A in a sequence of n, if the probability associated with it is

P(A) & = &p \P(\bar{A}) & = & 1-p

with the assumption that

p \ll 1 \quad 1-p \simeq 1

The probability of "k" events on a sequence of "n" not taking into account the order in which the "k" events happens can be expressed is:

\frac{1}{k!} \cdot \frac{n!}{(n-k)!} \cdot p^k(1-p)^{n-k}={n \choose k} p^k(1-p)^{n-k}

using the model of "n" numbers grouped by "k", not considering the order of the "k" outcome numbers in the group of "k" is the position of the "A" event on the sequence of "n", and there are %$k!$% different ways to order "k" numbers.

Considering the series expansion of the exponential function the following approximation hold

(1-p) \approx \exp(-p)

using the above assumption and considering "(n-k)" of the order of "n" result the Poisson Theorem

{n \choose k} p^k(1-p)^{n-k} \simeq \exp(-n p)\frac{(np)^k}{k!}

The probability Distribution of "k" A events on a sequence of "n" trials is:

P(k)= \exp(-n p)\frac{(np)^k}{k!}

Considering "n" as the count of "time unit" and using %$\lambda$% as the probability of the single event A and with the following random integer variable

%$ k(t) $%

the occurrence of k events after "t" time units, the following hold

P(k(t))= \exp(- \lambda t )\frac{(\lambda t)^k}{k!}

Poisson Distribution Characteristics

• maximum probability is at:

\lambda t =k

• Expected Value

E[ k ] = \lambda

• Variance

E[ (k-\lambda)^2 ] = \lambda

• Plot example

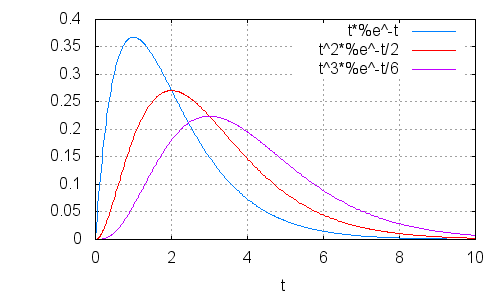
• Probability of interval

K(t+\tau)-K(t) & = & k \P( K(t+\tau)-K(t)) & = & \exp(- \lambda \tau )\frac{(\lambda \tau)^k}{k!}

Proactive Maintenace

• Preventive Maintenance is devoted to reduce component failure by scheduling components replacements associated with generalized life-expectancies. From established timetable routinely inspections are performed to detect maintenance problem. This strategy can be defined as Age-Dependent Repairs the age of the component "a" have to be known, repair renewal
• Condition Based Maintenance (Condition Monitoring) can improve the performance in term of cost and safe operation through the identification of pattern-to-failure trend; this is obtained by introducing testing techniques as Non Destructive Testing
• Predictive Maintenance involve the ability to use the data gathered in condition monitoring to answer to the following question: "how is the probability of failure for the analyzed components according to the future level of loads?"

-- RobertoBernetti - 02 Mar 2010