CinematicaDirettaManipolatore

Introduzione

La Cinematica Diretta di un manipolatore consiste nella determinazione delle equazioni che permettono di determinare la posizione finale dell'utensile terminale del braccio articolato in funzione delle rotazioni subite dai vari giunti. Raggiungere questo risultato richiede all'alunno la diretta sperimentazione dei seguenti processi:

• astrazione delle grandezze che descrivono il movimento (rotazione spostamento dei singoli compomenti giunti, snodi ecc..) , dal modello reale,
• applicare i concetti di Dominio, Codominio, Funzione alla descrizione del movimento
• uso delle proprietà algebriche delle operazioni per dedurre le proprietà del modello di descrizione del movimento del manipolatore

Il Movimento come "Relazione"

Nell'analisi di un manipolare si ha la necessità di descrivere quantitativamente il movimento dell'utensile terminale come può essere una pinza

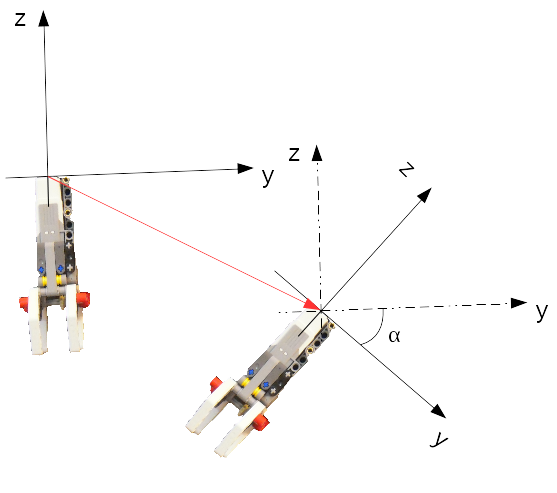Il processo di astrazione può iniziare associando alla pinza oggetti ideali come un sistema di riferimento ed alcuni punti. Immaginando di stendere sopra alla figura un foglio di carta velina e disegnandovi, in modo che risultino sovrapposti, gli elementi che compongono un sistema di riferimento (come nella figura precedente). Lo stesso procedimento può essere usato per associare dei punti a degli elementi particolari della pinza, come i punti \(\mathrm{A}\) e \(\mathrm{B}\).

I punti individuati sulla carta velina permettono di far corrispondere al movimento del foglio un movimento della pinza.

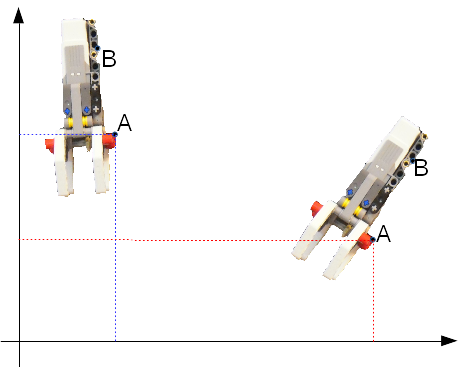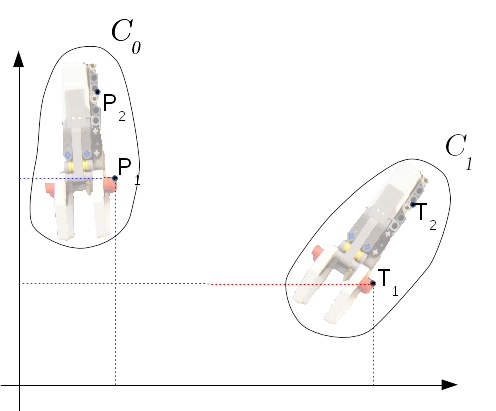
Si possono individuare quindi due insiemi di punti, che chiamiamo \( \mathrm{C_0} \) e \( \mathrm{C_1} \), che sono legati dalla relazione

"essere occupati dallo stesso punto della pinza in due istanti di tempo diversi"

Individuati i due istanti temporali, l'insieme \( \mathrm{C_0} \) è il Dominio mentre l'insieme \( \mathrm{C_1} \) è il Codominio della funzione \( f( \cdot) \) che algebricamente descrive tale relazione/funzione

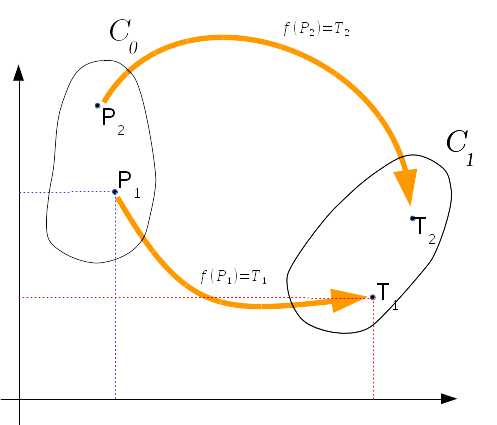
$$ T = f( P ) $$

Fissato quindi un dato istante temporale \( t \), il movimento della pinza mette in relazione fra loro diversi insiemi di punti.

Rappresentazione dei Punti e delle Funzioni

Continuiamo nel processo di descrizione attraverso la Matematica. I punti dello spazio che vengono via via occupati dai punti della pinza (disegnati sulla carta velina) possono essere rappresentati da una terna ordinata di valori, \( x \quad y \quad z \) alla quale assegnamo il nome della lettera con la quale abbiamo chiamato il punto:

$$ \mathbf{ P_1 } = \left[ \begin{array}{c} x_1 \\ y_1 \\ z_1 \\ \end{array} \right] $$

La traslazione può essere descritta sommando ad ogni elemento della tabella che rappresenta \(P_1\) lo spostamento \(Q\):

$$ \mathbf{ T_i } = \left[ \begin{array}{c} x_i \\ y_i \\ z_i \\ \end{array} \right] + \left[ \begin{array}{c} Q_{x} \\ Q_{y} \\ Q_z \\ \end{array} \right] $$

La rotazione rigida può invece essere descritta attraverso un prodotto tra una matrice ed un vettore come il seguente:

$$ \mathbf{ T_i } = \left[ \begin{array}{ccc} R_{11} & R_{11} & R_{11} \\ R_{21} & R_{22} & R_{23} \\ R_{11} & R_{11} & R_{33} \end{array} \right] \cdot \left[ \begin{array}{c} x_i \\ y_i \\ z_i \\ \end{array} \right] $$

Quindi sommando i due movimenti la funzione \( T = f( P ) \) è descritta algebricamente nel modo seguente

$$ \mathbf{ f( P ) } = \left[ \begin{array}{ccc} R_{11} & R_{12} & R_{13} \\ R_{21} & R_{22} & R_{23} \\ R_{11} & R_{11} & R_{33} \end{array} \right] \cdot \left[ \begin{array}{c} x \\ y \\ z \\ \end{array} \right] + \left[ \begin{array}{c} Q_{x} \\ Q_{y} \\ Q_z \\ \end{array} \right] $$

La Matrice di Rotazione

Dato un vettore \( \mathbf{\omega}_{0} \) parallelo alla retta attorno alla quale avviene la rotazione

$$ \mathbf{ \omega_0 } =\left[ \begin{array}{c} \omega_{0x} \\ \omega_{0y} \\ \omega_{0z} \\ \end{array} \right] $$

La matrice di rotazione è data dalla seguente formula di Rodriguez

$$ \mathbf{R} = \mathbf{I} + \widehat{ \mathbf{\omega} }_{0} \cdot \sin{\theta} + \left( 1 - \cos(\theta) \right) \cdot \widehat{ \mathbf{\omega} }_{0}^2 $$

dove:

• \(\theta\) è l'angolo di rotazione rigida subita dalla pinza
• \(\widehat{ \mathbf{\omega} }_{0} \) è una matrice costruita dalle componenti del vettore \( \mathbf{\omega}_{0} \) nel modo seguente:

$$ \widehat{ \mathbf{\omega} }_{0} = \left[ \begin{array}{ccc} 0 & -\omega_{0z} & \omega_{0y} \\ \omega_{0z} & 0 & -\omega_{0x} \\ -\omega_{0y} & \omega_{0x} & 0 \end{array} \right] $$

Prendiamo in considerazione il braccio realizzabile con il kit EV3 in figura:

Ogni componente

1. prima asta fissa
2. seconda asta mobile
3. pinza

subisce gli stessi spostamenti (traslazioni e rotazioni) del componente a cui è legato. Associando ad ogni giunto un sistema di riferimento, nell'esempio in questione avremmo tre sistemi inizialmente sovrapposti, ognuno dei quali subisce prima una traslazione e poi ina rotazione.

Traslazione rispetto al giunto che lo precede nella catena

Traslazione
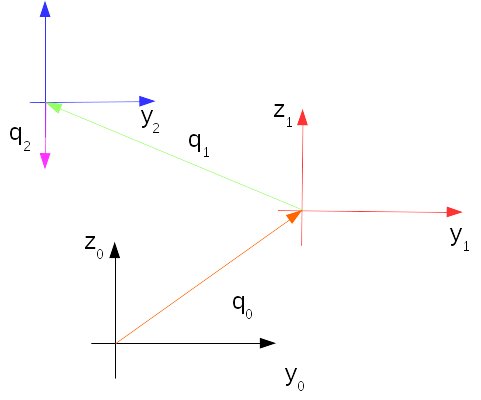Il processo di astrazione può proseguire nella foto seguente dove i vettori \( q_i \) vengono sovrapposti al manipolatore "Lego", con i relativi valori misurati con "tracker" (programma di analisi video)

I vettori \( q_i \) possono essere rappresentati alegricamente nel modo seguente:

$$\mathbf{q_{0}} = \left[ \begin{array}{c} 0 \\ l_{y0} \\ l_{z0} \\ \end{array} \right] $$

$$\mathbf{q_{1}} = \left[ \begin{array}{c} 0 \\ l_{y1} \\ 0 \\ \end{array} \right] $$

$$\mathbf{q_{2}} = \left[ \begin{array}{c} 0 \\ 0 \\ -l_{z2} \\ \end{array} \right] $$

Rotazione attorno all'asse del giunto

Rotazione

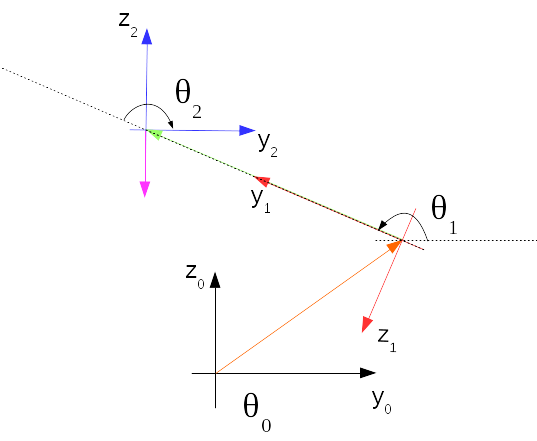Si deve notare che nel caso del manipolatore in figura l'utensile di estremità, una pinza, resta allineato alla verticale vale quindi la seguente condizione tra le ultime due rotazioni: $$ \theta_2 = -\theta_1 $$

I versori degli assi delle rotazioni sono dati dai seguenti vettori:

$$ \mathbf{ \omega_0 } =\left[ \begin{array}{c} 0 \\ 0 \\ 1 \\ \end{array} \right] $$

$$ \mathbf{ \omega_1 } =\left[ \begin{array}{c} 1 \\ 0 \\ 0 \\ \end{array} \right] $$

$$ \mathbf{ \omega_2 } =\left[ \begin{array}{c} 1 \\ 0 \\ 0 \\ \end{array} \right] $$

Applicando la formula di Rodriguez vista in precedenza si ottengono le seguenti matrici:

• per la rotazione 0

$$ \mathbf{R}_0 = \left[ \begin{array}{ccc} \cos{\theta_0} & -\sin{\theta_0} & 0 \\ \sin{\theta_0} & \cos{\theta_0} & 0 \\ 0 & 0 & 1 \end{array} \right] $$

• per la rotazione 1

$$ \mathbf{R}_1 = \left[ \begin{array}{ccc} 0 & 0 & 1 \\ 0 & \cos{\theta_1} & -\sin{\theta_1}\\ 0 & \sin{\theta_1} & \cos{\theta_1} \end{array} \right] $$

• per la rotazione 2

$$ \mathbf{R}_2 = \left[ \begin{array}{ccc} 0 & 0 & 1 \\ 0 & \cos{(-\theta_1)} & -\sin{(-\theta_1)}\\ 0 & \sin{(-\theta_1)} & \cos{(-\theta_1)} \end{array} \right] $$

Composizione delle rotazioni

La posizione della punta del vettore \( \mathbf{q_{2}} \) rispetto al sistema di riferimento globale a questo punto può essere ottenuta componendo i vari movimneti, quindi:

• la posizione di \( \mathbf{q}_{2} \) rispetto al sistema 1

$$ \mathbf{x_2} = \mathbf{q}_{1} + \mathbf{R}_2 \cdot \mathbf{q}_{2} $$

• la posizione del vettore ruotato \( \mathbf{x_2} \) rispetto al sistema 0

$$ \mathbf{x_1} = \mathbf{q}_{0} + \mathbf{R}_1 \cdot \mathbf{x_2} $$

• la rotazione del sistema 0 rispetto al sistema globale

$$ \mathbf{x_0} = \mathbf{R}_0 \cdot \mathbf{x_1} $$

---

Sostituendo a cascata la prima equazione nella seguente e così via si ottiene la seguente espressione (dopo aver raccolto opportunamente le funzioni trigonometriche) :

$$\mathbf{x_0} =\pmatrix{-\sin \left(\vartheta_{0}\right)\cdot \left(l_{\mathrm{y0}}- \sin \left(\vartheta_{1}\right)\cdot \left(\cos \left(\vartheta_{1} \right)\cdot l_{\mathrm{z2}}-\sin \left(\vartheta_{1}\right)\cdot l_{ \mathrm{y2}}\right)+\cos \left(\vartheta_{1}\right)\cdot \left(\sin \left(\vartheta_{1}\right)\cdot l_{\mathrm{z2}}+\cos \left(\vartheta_{1} \right)\cdot l_{\mathrm{y2}}+l_{\mathrm{y1}}\right)\right)\cr \cos \left(\vartheta_{0}\right)\cdot \left(\cos \left(\vartheta_{1}\right)\cdot \left(l_{\mathrm{y1}}+\cos \left(\vartheta_{1}\right)\cdot l_{ \mathrm{y2}}+\sin \left(\vartheta_{1}\right)\cdot l_{\mathrm{z2}}\right) -\sin \left(\vartheta_{1}\right)\cdot \left(\cos \left(\vartheta_{1} \right)\cdot l_{\mathrm{z2}}-\sin \left(\vartheta_{1}\right)\cdot l_{ \mathrm{y2}}\right)+l_{\mathrm{y0}}\right)\cr \sin \left(\vartheta_{ 1}\right)\cdot \left(l_{\mathrm{y1}}+\cos \left(\vartheta_{1}\right)\cdot l _{\mathrm{y2}}+\sin \left(\vartheta_{1}\right)\cdot l_{\mathrm{z2}} \right)+\cos \left(\vartheta_{1}\right)\cdot \left(\cos \left(\vartheta _{1}\right)\cdot l_{\mathrm{z2}}-\sin \left(\vartheta_{1}\right)\cdot l_{ \mathrm{y2}}\right)+l_{\mathrm{z0}}\cr }$$

Usando la principale identità trigonometrica il vettore \( \mathbf{x_0} \) diventa:

$$\mathbf{x_0} = \pmatrix{-\sin \left(\vartheta_{0}\right)\cdot l_{\mathrm{y2}}-\sin \left(\vartheta_{0}\right)\cdot \cos \left(\vartheta_{1}\right)\cdot l_{ \mathrm{y1}}-\sin \left(\vartheta_{0}\right)\cdot l_{\mathrm{y0}}\cr \cos \left(\vartheta_{0}\right)\cdot l_{\mathrm{y2}}+\cos \left( \vartheta_{0}\right)\cdot \cos \left(\vartheta_{1}\right)\cdot l_{ \mathrm{y1}}+\cos \left(\vartheta_{0}\right)\cdot l_{\mathrm{y0}}\cr l_{ \mathrm{z2}}+l_{\mathrm{z0}}+\sin \left(\vartheta_{1}\right)\cdot l_{ \mathrm{y1}}\cr }$$

e raccogliendo i fattori comuni:

$$\mathbf{x_0} = \pmatrix{-\sin \left(\vartheta_{0}\right)\cdot \left(l_{\mathrm{y0}}+ \cos \left(\vartheta_{1}\right)\cdot l_{\mathrm{y1}}+l_{\mathrm{y2}} \right)\cr \cos \left(\vartheta_{0}\right)\cdot \left(l_{\mathrm{y2}}+ \cos \left(\vartheta_{1}\right)\cdot l_{\mathrm{y1}}+l_{\mathrm{y0}} \right)\cr l_{\mathrm{z2}}+l_{\mathrm{z0}}+\sin \left(\vartheta_{1} \right)\cdot l_{\mathrm{y1}}\cr }$$

Usando in modo opportuno le formule di addizione e sottrazione si può ottenere la seguente espressione:

$$\mathbf{x_0} =\pmatrix{-\sin \left(\vartheta_{0}\right)\cdot l_{\mathrm{y2}}-{{\sin \left(\vartheta_{1}+\vartheta_{0}\right)\cdot l_{\mathrm{y1}}}\over{2}}+ {{\sin \left(\vartheta_{1}-\vartheta_{0}\right)\cdot l_{\mathrm{y1}} }\over{2}}-\sin \left(\vartheta_{0}\right)\cdot l_{\mathrm{y0}}\cr \cos \left(\vartheta_{0}\right)\cdot l_{\mathrm{y2}}+{{\cos \left(\vartheta_{ 1}+\vartheta_{0}\right)\cdot l_{\mathrm{y1}}}\over{2}}+{{\cos \left( \vartheta_{1}-\vartheta_{0}\right)\cdot l_{\mathrm{y1}}}\over{2}}+\cos \left(\vartheta_{0}\right)\cdot l_{\mathrm{y0}}\cr l_{\mathrm{z2}}+l_{ \mathrm{z0}}+\sin \left(\vartheta_{1}\right)\cdot l_{\mathrm{y1}}\cr }$$

Le precedenti formule permettono di determinare le coordinate del punto occupato dal centro del manipolatore rispetto al sistema di riferimento globale.

Cinematica Inversa

E' importante poter determinare note le coordinate del punto i valore di \( \theta_0 \) e \( \theta_1\) corrispondenti a tale scopo le equazioni precedenti possono essere rappresentate nel piano cartesiano in modo da poter risolvere graficamente l'equazione inversa.

Coordinate nel Sistema Globale Centro Pinza

Coordinata Y Globale

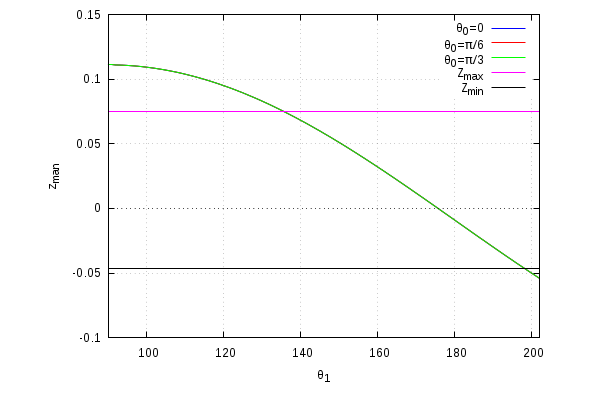Coordinata Z Globale

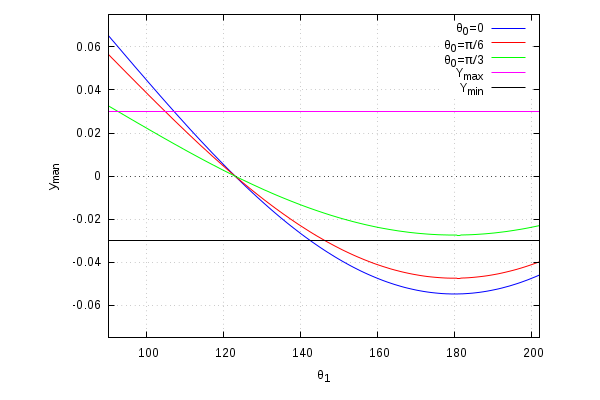Coordinata X Globale

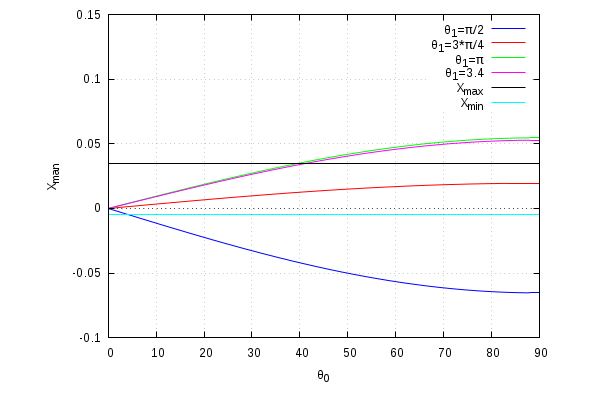Coordinate nel Sistema Giunto Braccio Pinza

Coordinata Y Globale

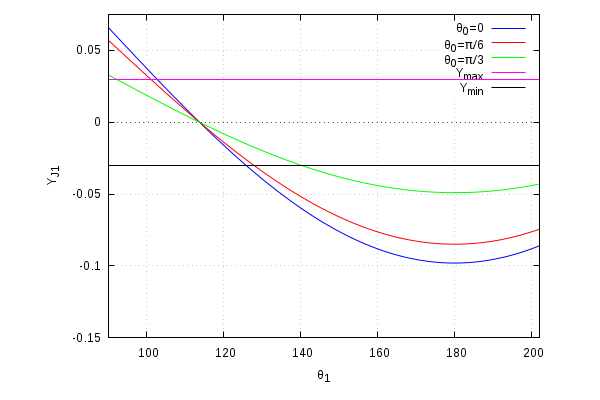Coordinata Z Globale

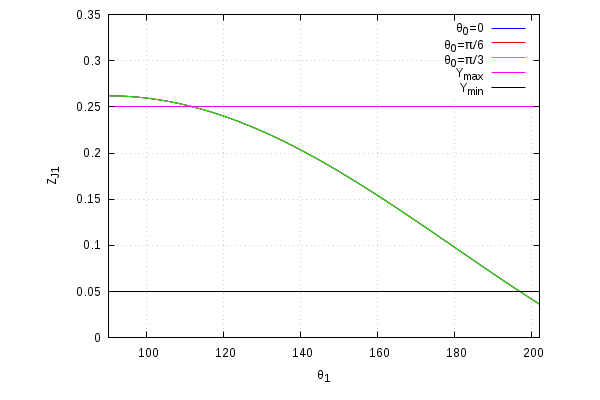Fine

-- RobertoBernetti - 07 Dec 2015